Scurtături importante
| Treci pe tot ecranul: | F11 (majoritatea browserelor) |
| Anulează mișcare: | Ctrl+Z |
| Împarte din nou cărțile: | F2 |
| Închide casetă de dialog: | Esc |
Freecell
Bun venit la Freecell Solitaire! Aceasta este o versiune online gratuită a popularului joc de cărți. Distracție plăcută!
Prezentare generală
Freecell este un joc de cărți jucat de un singur jucător. Ca majoritatea tipurilor de solitaire, în Freecell obiectivul este să sortezi cărțile după suită și valoare. Totuși, spre deosebire de un Solitaire tradițional, toate cărțile sunt cu fața în sus de la începutul jocului și nu există un pachet. De asemenea, mâinile de Freecell sunt aproape întotdeauna rezolvabile. De aceea, este dificil să consideri rezultatul jocului ca un semn bun sau prost, cum se face de obicei în solitaire-ul tradițional.
Tabla de joc constă din opt coloane în mijloc, patru celule libere în colțul din stânga sus și patru baze în colțul din dreapta sus. Pentru a câștiga jocul, trebuie să muți cărțile între coloane și să le aranjezi secvențial, în culori alternative. Poți folosi celulele libere din colțul din stânga sus al tablei pentru a stoca temporar cărți în ele. În final trebuie să pui toate cărțile în baze, începând cu ași, doiari, treiari etc. Fiecare stivă dintr-o bază trebuie să conțină doar cărți dintr-o singură suită.
Reguli
Mutarea cărților între coloane
- Poți lua cartea de deasupra coloanei sau poți lua un șir de cărți, atât timp cât sunt în ordine secvențial (după valoare) ți au culori alternative (negru și roșu).
- Poți pune o carte (sau un șir de cărți) deasupra altei cărți, atât timp cât cartea de destinație are valoarea mai mare cu unu și este de culoarea opusă cărții pe care o muți (sau a cărții de la baza șirului pe care-l muți). Ceea ce înseamnă că este posibil să pui o carte neagră peste o carte roșie și invers. Reține că este imposibil să pui un popă peste altă carte, deoarece nicio carte nu are o valoare mai mare decât popa.
- Dacă o coloană e goală, poți pune în ea orice carte.
- Dacă muți un șir de cărți, trebuie să te asiguri că există suficiente celule libere pentru a facilita mișcarea. Aceasta se întâmplă deoarece, în Freecell, cărțile pot fi mutate numai una câte una. Dacă muți un șir, se petrece ca și cum ai fi folosit celulele libere pentru a stoca temporar cărțile în timp ce dezasamblezi șirul într-o coloană și apoi îl reasamblezi în altă coloană. Acest lucru ar fi destul de plictisitor, așa că programul îți permite să muți întregul șir, decât să muți cărțile una câte una. Totuși jocul calculează întotdeauna dimensiunea maximă a șirului care poate fi mutat, având în vedere situația actuală. Formula pentru dimensiunea maximă a șirului include numărul de celule libere în colțul din stânga sus și numărul de coloane libere.
- Există posibilitatea de a muta șiruri mai lungi decât cele premise d numărul de celule libere și de coloane libere. De exemplu, dacă în altă coloană descoperi o carte pe care poți stoca temporar o parte din șirul tău, poți să o folosești pentru a-ți împărți șirul în două și a mișca separate cele două jumătăți.
Folosirea celulelor libere
- Există patru celule libere.
- Fiecare celulă liberă poate conține o singură carte.
- Orice carte poate fi plasată pe o celulă liberă.
- Numărul de celule libere disponibile este folosit pentru a calcula dimensiunea maximă a șirului pe care-l poți muta în prezent.
Bazele
- Există patru baze: câte una pentru fiecare suită. Fiecare bază poate conține doar cărți dintr-o singură suită.
- Prima carte plasată în fiecare bază trebuie să fie un as. Asul este o carte de bază.
- Odată ce asul a fost plasat în bază, poți plasa acolo doar o carte cu valoarea mai mare cu exact unu. În acest mod, sortezi cărțile secvențial ascendent după valoare și suită.
- Odată ce toate cărțile au fost plasate pe baze, jocul a fost câștigat!
Informații suplimentare
- Uneori, cărțile vor fi trimise automat în baze. Doar cărțile care nu pot fi utile pentru sortarea coloanelor sunt trimise automat în baze.
- Poți trimite forțat o carte în bază dând clic dreapta pe acea carte.
- Poți trimite forțat în baze toate cărțile corespunzătoare dând clic dreapta pe zona verde din partea de jos a tablei de joc.
- O durată bună în care să câștigi jocul este de 3 minute.
- Freecell nu are un sistem de ținere a scorului. Pentru jucătorii începători, măsura performanței poate fi numărul de cărți rămase pe tablă (adică, nu în baze) la momentul în care se blochează și renunță. Pentru jucătorii care tind să rezolve mai des jocurile, măsura performanței pentru un singur joc poate fi durata de timp cât au jucat. Procentul de jocuri câștigate le poate indica performanța totală.
Exemplu de rezolvare
Iată un exemplu de mod de a începe cu succes rezolvarea unui joc de Solitaire Freecell.
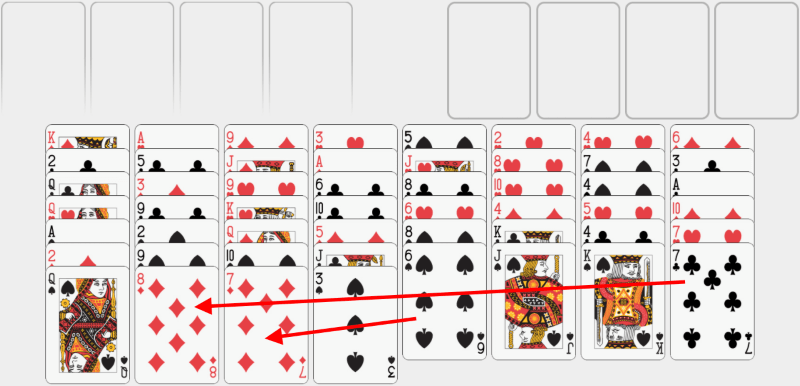 În această mână, la suprafață nu există ași. Totuși, putem muta niște cărți pentru a ajunge la ei. Începem prin a pune 7 de treflă pe 8 de caro și 6 de pică pe 7 de caro. Reține că putem amplasa o carte doar pe alta care are valoarea cu unu mai mare și care trebuie să fie de culoarea opusă. Ceea ce înseamnă că putem pune cărțile roșii (caro și cupă) pe cărțile negre (pică și treflă) și invers. |
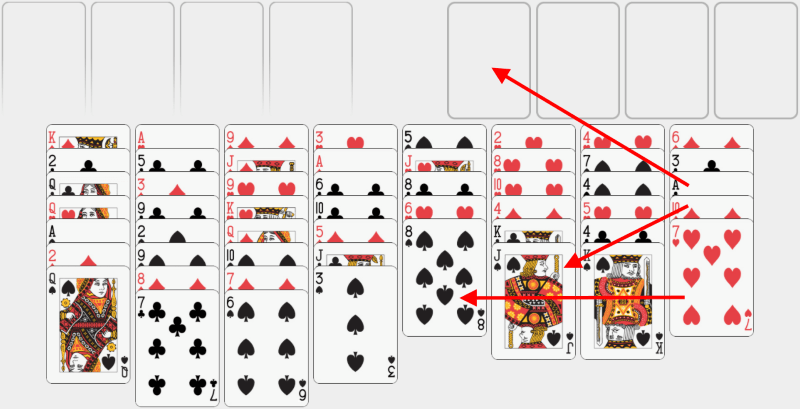 Acum să ne concentrăm pe cea mai din dreapta coloană. Putem muta 7 de cupă pe 8 de pică și 10 de caro pe valetul de pică. Astfel descoperim asul de treflă, pe care-l putem pune în prima bază. |
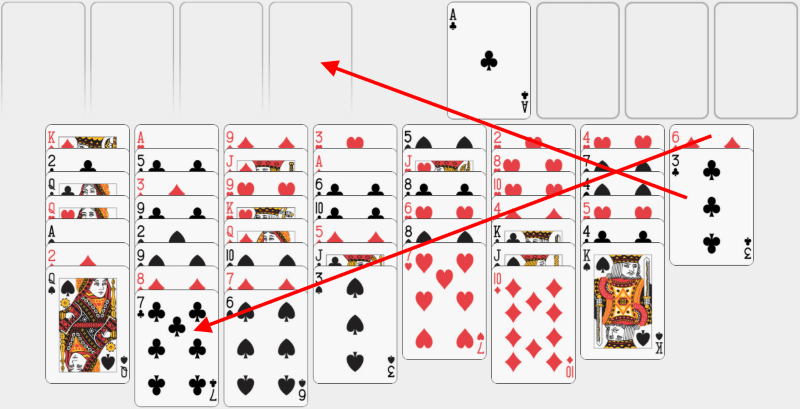 Continuăm să ne concentrăm pe cea mai din dreapta coloană. Putem muta 3 de treflă într-una din celulele libere și apoi să punem 6 de caro pe 7 de treflă. Astfel eliberăm coloana cea mai din dreapta. Este de dorit să avem o coloană goală, deoarece o putem folosi nu doar ca o celulă liberă adițională, ci și pentru a construi în ea șiruri de cărți. |
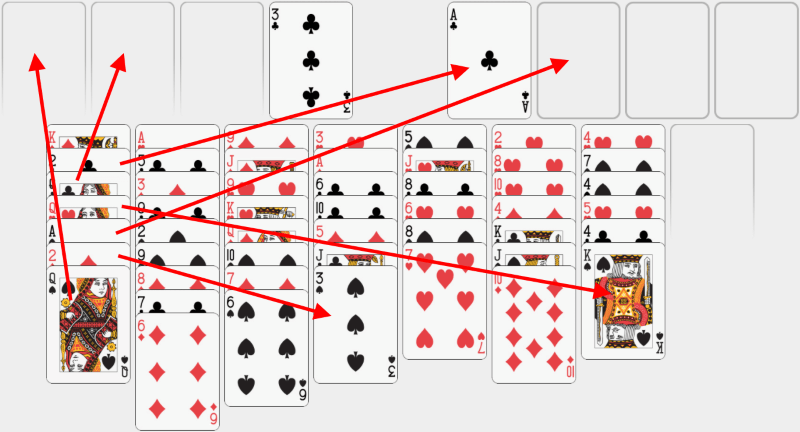 Acum putem încerca să dezasamblăm cea mai din stânga coloană. Putem să o facem punând dama de pică într-o celulă goală, 2 de caro pe 3 de pică, asul de pică în cea de-a doua bază, dama de cupă pe popa de pică, dama de treflă într-o celulă liberă și 2 de treflă pe asul de treflă (care se află deja în bază). Pare că ne-am aglomerat tabla de joc – acum avem ocupate trei din cele patru celule libere. Dar nu te teme! Vei vedea în curând că am gândit strategic și vom recupera ușor claritatea tablei de joc. |
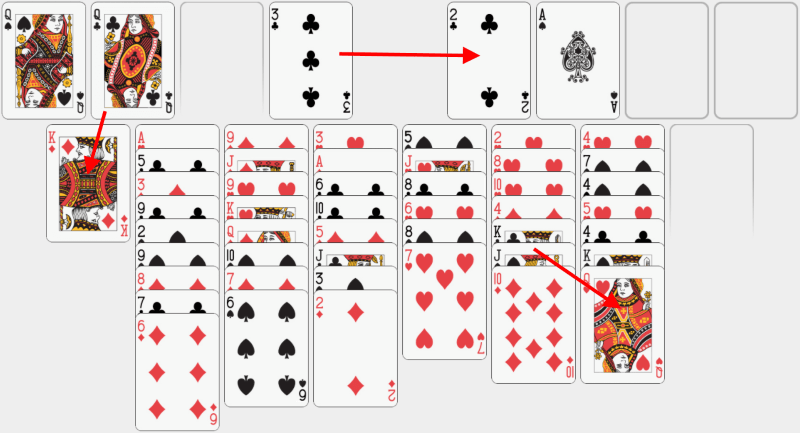 Să mutăm dama de treflă pe popa de caro și 3 de treflă pe 2 de treflă. Putem muta și un șir mic alcătuit din două cărți: valetul de pică și 10 de caro. Să luăm aceste cărți și să le punem pe dama de cupă. Acum tabla de joc arată din nou ordonată! |
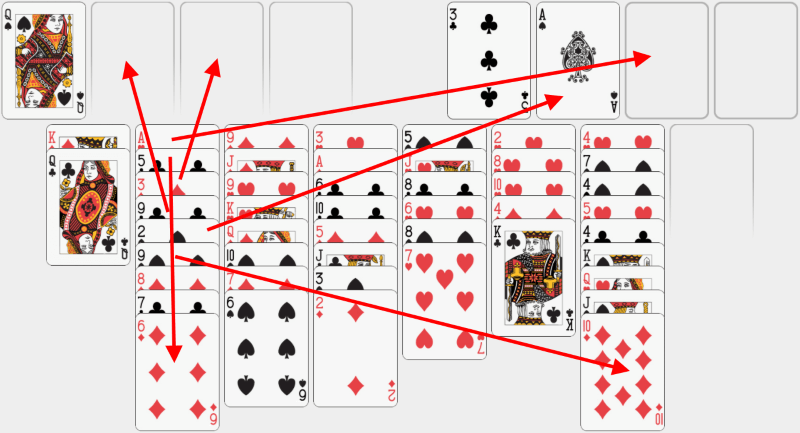 De data aceasta ne vom concentra pe cea de-a doua coloană. Observă că există un șir care conține patru cărți, cu 9 de treflă la bază. Putem muta întregul șir pentru a-l pune peste 10 de caro. Astfel avem acces la 2 de pică, pe care-l putem pune peste asul de pică. 9 de treflă, împreună cu 3 de caro, pot fi acum transferate în celulele libere disponibile. 5 de treflă poate fi pus peste 6 de caro, care se află acum în cea de-a șaptea coloană. Aceasta ne permite să ne atingem obiectivul: acces la asul de cupă, pe care-l putem pune pe următoarea bază disponibilă. |
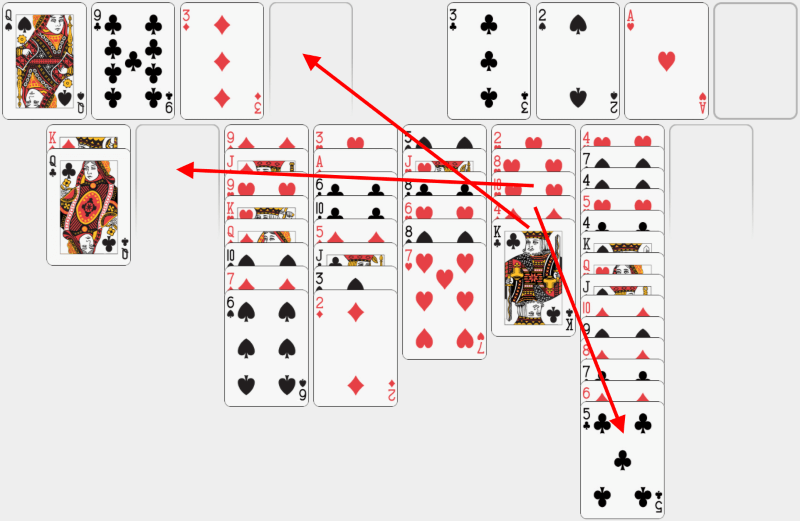 Pare a fi o idee bună să ne concentrăm mai departe pe coloana a șasea. Așa că mutăm popa de treflă în ultima celulă liberă rămasă, 4 de caro pe 5 de treflă și 10 de cupă în coloana a doua, care este goală. |
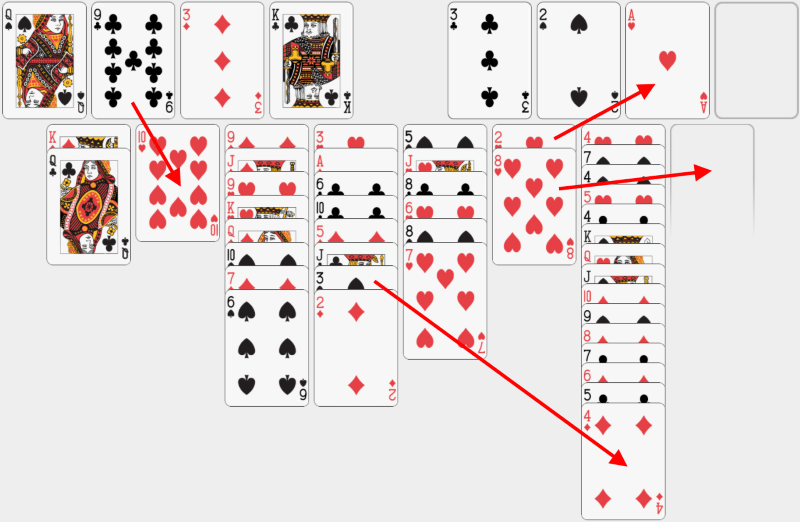 Punem 9 de treflă pe 10 de cupă și 8 de cupă în coloana a opta, care este goală. Avem astfel acces la 2 de cupă, pe care-l putem apoi pune în bază cu asul de cupă. În final, punem șirul de două cărți care începe cu 3 de pică pe 4 de caro. |
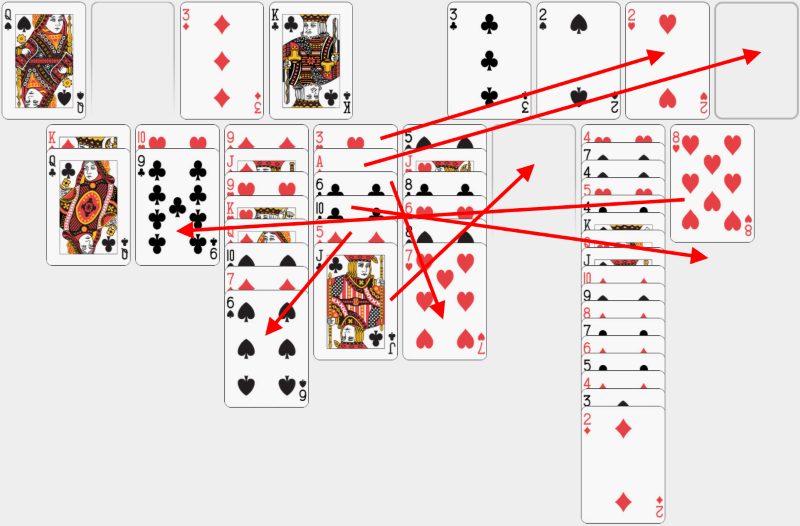 Acum vom încerca să dezasamblăm cea de-a patra coloană. Mai întâi, să punem valetul de treflă în ultima coloană liberă rămasă. Apoi punem 5 de caro pe 6 de pică. Trebuie să îndepărtăm 8 de cupă din coloana a opta și să-l punem pe 9 de treflă. Apoi putem pune 10 de treflă în coloana nou-golită. Acum putem pune 6 de treflă pe 7 de cupă și să câștigăm acces la asul de caro. Putem să-l punem pe ultima bază rămasă. Și, în final, putem pune 3 de cupă pe 2 de cupă în bază. Reține că 2 de caro a fost trimis automat în bază, deoarece nu a mai rămas nimic pe tablă de pus peste el. |
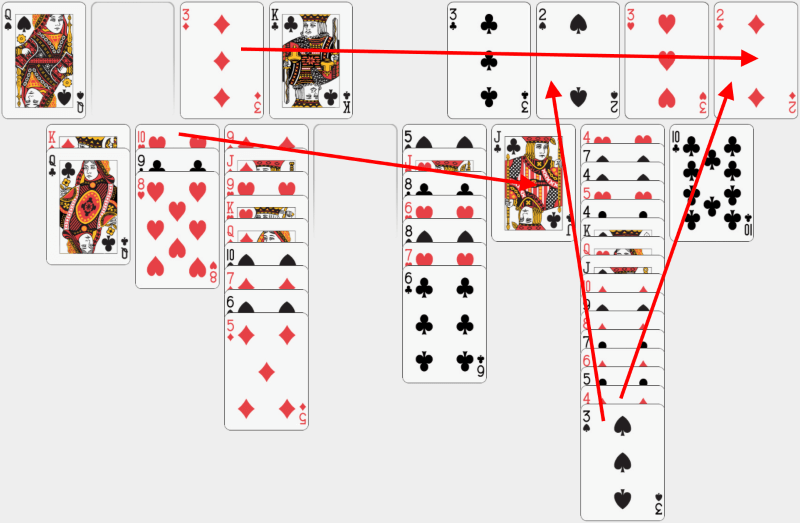 Acum să facem curat. Mai întâi punem 3 de caro din celula liberă pe 2 de caro din bază. Apoi putem muta șirul care începe cu 10 de cupă și să-l punem pe valetul de treflă. În final, putem muta 3 de pică și 4 de caro în bazele corespunzătoare. |
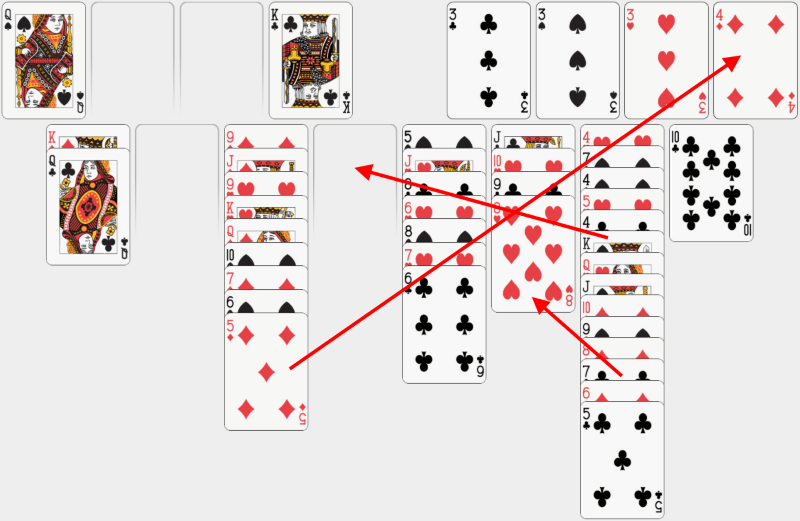 Acum vom face o mișcare complicată. Dar, mai întâi, să mutăm 5 de caro pe 4 de caro. După ce l-am dat din drum, vrem să mutăm șirul gigant care începe cu popa de pică într-o coloană goală, ca să putem avea acces la toate cărțile din coloana a șaptea. Din păcate, nu sunt destule celule libere și coloane goale disponibile pentru a efectua această operațiune. Din fericire, avem o posibilitate! Putem împărți acest șir uriaș în două: putem muta șirul lung de trei cărți care începe cu 7 de treflă pe 8 de cupă și apoi să mutăm șirul rămas (care începe cu popa de pică) în coloana liberă. |
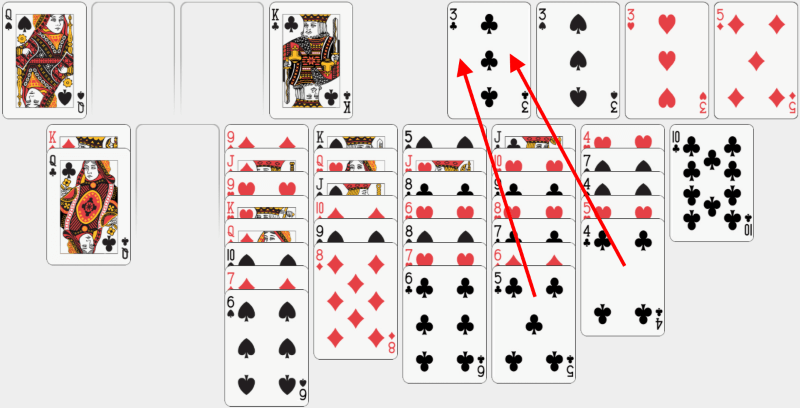 Mutăm 4 de treflă în bază. Apoi facem același lucru cu 5 de treflă. |
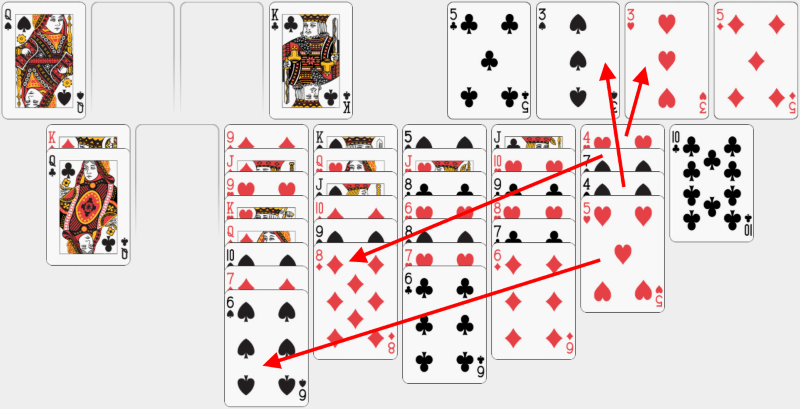 În final putem dezasambla cea de-a șaptea coloană. Punem 5 de cupă pe 6 de pică, 4 de pică pe 3 de pică și 7 de pică pe 8 de caro. În final, punem 4 de cupă pe 3 de cupă. |
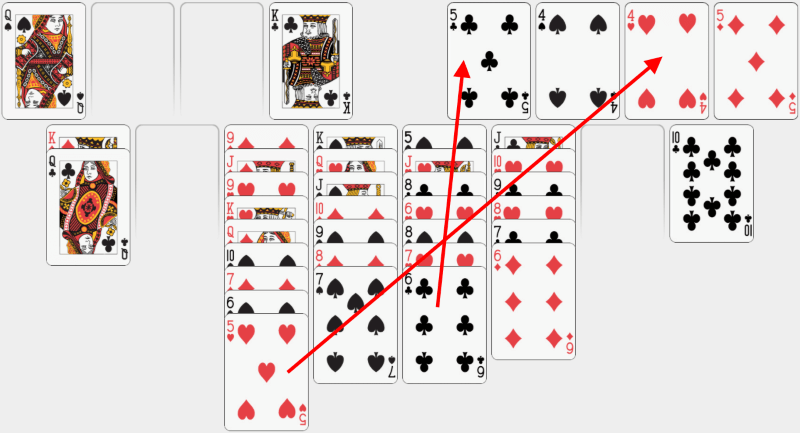 Să umplem și bazele puțin. Mutăm 6 de treflă pe 5 de treflă. Apoi 5 de cupă pe 4 de cupă. |
 Acum avem două celule libere și două coloane goale. Cărțile sunt deja sortate destul de bine și e clar că jocul poate fi rezolvat. De acum înainte, va fi din ce în ce mai ușor. Bună treabă! :) |
Istorie
Solitare Freecell își poate găsi originea în anul 1968, când în Scientific American a fost publicat un joc ușor diferit. Acest joc a fost modificat, devenind Freecell, și implementat pentru prima dată pentru computere în 1978. Totuși, Freecell a putut câștiga popularitate deoarece a fost inclus în fiecare copie de Microsoft Windows din 1995. Originalul jocului Microsoft Freecell avea 32.000 de mâini numerotate. Între 1994 și 1995 a existat un proiect pentru rezolvarea tuturor celor 32.000 de mâini și s-a dovedit că numai una dintre ele nu putea fi rezolvată. Din acel moment, Freecell a devenit cunoscut drept jocul care poate fi rezolvat aproape întotdeauna.